The Polarization is one of the three degrees of freedom by which the complex vector field of the light is defined. With scalar approximation, that is treating the light propagation via scalar wave equation, the effects related to the polarization of the light is ignored. As a result, the light beam is considered as scalar, and not vector, field defined with two parameters of intensity and phase. Clearly, “direction” is what makes the vector wave field different from a scalar field. In some cases, mostly with uniform polarization, it would be possible to treat the light as scalar field. However, there are situations in which the polarization might change throughout the wavefield. Moreover, for exploring some properties in the light-matter interaction experiments (like the orientation of the molecules) manipulating the light polarization is necessary. But, what is “polarization”?
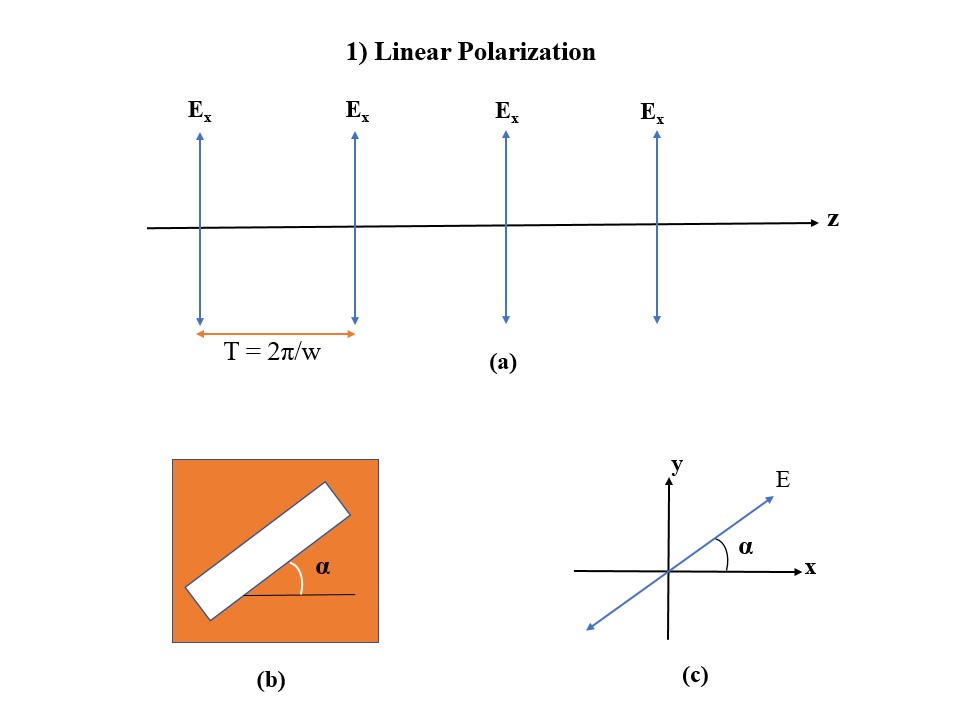
Polarization defines how and in which orientation the Electric Field vibrates in a page vertical to the propagation axis. For example, Figure (1a) shows the electric field vibrating in the x-direction vertical to propagation axis (z); In this case, it is said that electric field has a linear polarization. The electric field with linear polarization can posses both components of Ex and Ey with different amplitudes; Polarizers are simple devices that produce and manipulate different linear polarization by superposing these two states in a plane inclined at an particular angle (b-c). They only change the amplitude, and not the phase, of the light field passing through them. As a result, there is no phase difference between two orthogonal components of a linearly polarized light field.
With adding a phase difference between basis orthogonal polarization states in a linearly polarized light (Electric field), a wave field with new properties is produced. A phase difference of pi/2, for instance, produces an elliptical polarization as shown in figure 2. A polarization ellipse, in addition to magnitude and phase of the horizontal and vertical components of Electric field, has also some geometrical parameters characterized by ellipticity and the angle by which the orientation of the ellipse is defined. The circular polarization is a special case of elliptical polarization when the magnitudes of horizontal and vertical components are the same. These three states of polarizations (SoPs) can be simply described and visualized through a convenient geometric representation known as Poincare Sphere. As shown in Figure 2, it’s a unit sphere with s1, s2, and s3 as Stokes parameters of a point on the sphere in Cartesian coordinate system. The latitude and longitude angles at each point define the ellipticity and orientation of the polarization ellipse. For instance, the points 1 & 2 on the sphere demonstrate the same ellipticity simply because they are placed on the same latitudinal circle. They have, however, various orientation; The state of polarization at point 1 is horizontal ellipse because its longitude angle is zero. That is the case for every point placed on this meridian. The elliptical polarization at point 2, on the other hand, is rotated around its horizontal axis. The linearly and circularly polarized fields are two special cases of light field. The state of polarization at any point in the equator of the sphere is linear. Every other point on the sphere represents an elliptical polarization except for two poles which are demonstrative of circularly polarized field. The positive and negative sides of the ellipse stand for right-hand and left-hand polarization, respectively. Generally, these three well-known state of polarizations (SoPs)- linear, elliptical, and circular, are homogenous. That is to say, the state of polarizations at different locations of the field cross section are identical.


With engineering and structuring the state of polarization at various location of the field cross-section, vector fields with inhomogeneous local polarization states with unique properties and applications can be produced. The most typical vector fields are radially and azimuthally polarized fields; Radially polarized fields (Figure 3a) have all the local state of polarizations arranged along the radial direction in the field cross section. When focused, they can produce sharper focal spot than that of a scalar field. The Azimuthally polarized field (Figure 3b) can be focused into a hollow dark spot. The vector fields with cylindrically symmetric polarization can also exhibit other structures and forms, as depicted in figure 3c & 3d.

As in the case of scalar field, singularities can be also appeared in a vector field known as vectorial vortex. While singularities in scalar field are produced by the undefined or abrupt change in phase or the amplitude of the wave, the vectorial vortex can appear (figure 4) when we allow the polarization to be space-varying;